生産者から見たミクロ経済学
財を供給する→供給曲線の導出
労働力と資金を需要する→需要曲線の導出
生産関数
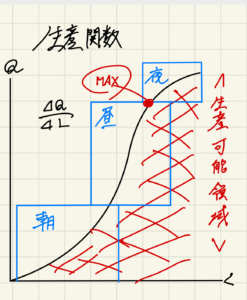
労働Lや資本Kの生産要素の投入量と生産量Qの対応関係を表すもの。
Q＝f(K,L) （QはK,Lの関数）
・限界生産力
労働が1単位増加した際にどれだけ生産量が増えるのか
MPL=ΔQ/ΔL
※労働の限界生産力逓減の法則によりある点を境に傾きが緩やかになる。
等利潤線と最適生産
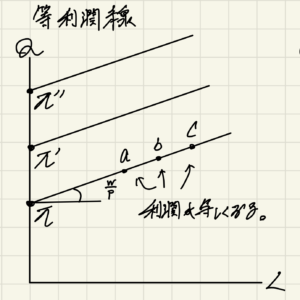
π=P・Q －（w・L＋r・K）
Π：利潤 P：価格 Q：生産量 w：賃金率 L：労働量 r：利子率 K：資本量
Q＝w/P・L＋π/P（傾き＋切片）
・費用関数
生産量Qと費用Cの対応関係を表すもの。
C＝f(Q)
変動費用曲線
短期総費用関数
固定費（VC）：減価償却費等
変動費（TC）：人件費等。（生産量に伴って人件費が変動する）
平均費用（AC）
総費用（TC）を生産量Qで除したもの。（傾き）
平均可変費用
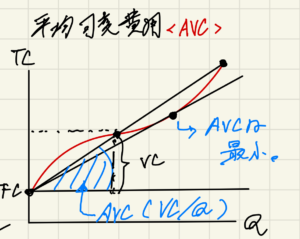
平均可変費用（AVC）
変動費用（VC）を生産量Qで除したもの。（傾き）
限界費用
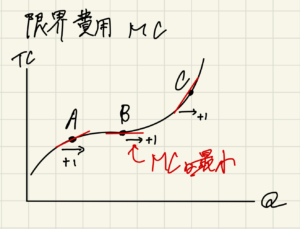
限界費用（MC)
総費用曲線上の任意の1点における接線の傾き。（生産量が1増えたときに費用がいくら増加するのか）
★AC、AVCの最小点はMCとの交点。
利潤最大化条件
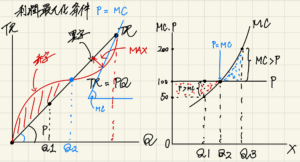
P＝MC
価格＝限界費用の時、利潤は最大化する。
（総費用曲線と総収入曲線TRの乖離幅が最大の点）
超過利潤
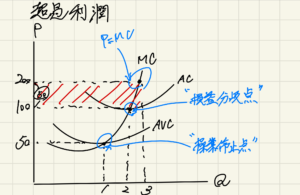
★利潤ゼロの場合も株主への配当金等は費用として折り込んでいる（利益は出ている）
→利潤ゼロを超えているので「超過利潤」と表現している。
◎損益分岐点・操業停止点
損益分岐点：利潤ゼロ
操業停止点：収入が平均可変費用を下回っている